Модуль числа, або абсолютне значення, перетворює будь-яке число на його “позитивну копію”, ніби стирає знак мінус одним махом. Щоб знайти модуль |x|, перевірте знак: якщо x дорівнює або перевищує нуль, то |x| = x. Для негативних значень просто помножте на -1, і отримаєте |x| = -x. Наприклад, |7| лишається 7, а |-3| стає 3 – просто і блискавично.
Ця проста операція ховає в собі потужний інструмент для математики, програмування та навіть фізики. На числовій прямій модуль вимірює відстань від точки до нуля, ігноруючи напрямок. Розберемося глибше, з прикладами, щоб ви могли впевнено розв’язувати задачі будь-якої складності.
Уявіть, як мінус зникає, ніби тінь від сонця: число стоїть на своєму місці, але його величина сяє яскраво. Тепер зануримося в деталі, де кожен крок пояснений з прикладами та хитрощами.
Що таке модуль числа: суть поняття
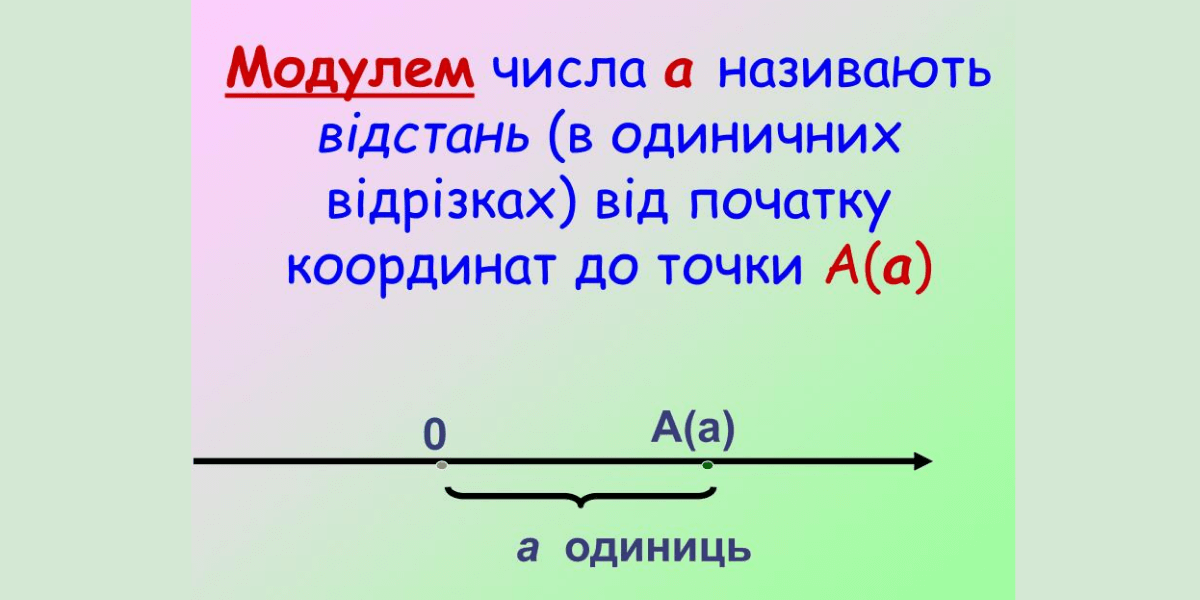
Модуль числа позначається вертикальними рисками |x| і завжди невід’ємний – від 0 до нескінченності. Це фундаментальна ідея в математиці, яка з’являється вже в 6 класі шкільної програми, але продовжує служити в університетських рівняннях і коді. Згідно з визначенням з uk.wikipedia.org, модуль |a| дорівнює довжині відрізка від початку координат до точки, що відповідає числу a на числовій осі.
Для раціональних чисел правило просте: візьміть дроби чи десяткові – принцип той самий. |2.5| = 2.5, а |-1/2| = 1/2. Цікаво, що модуль нуля дорівнює нулю, бо відстань до себе – нульова. Це правило діє для всіх дійсних чисел, від цілих до ірраціональних, як √2 чи π.
Чому це важливо? Бо модуль стирає знак, фокусуючись на величині. У повсякденному житті ми постійно думаємо про “скільки”, а не “куди” – скільки кілометрів до міста, незалежно від напрямку.
Геометричний сенс модуля: відстань без напрямку
На числовій прямій, де нулі – центр світу, кожне число ховається в точці. Модуль – це просто кількість кроків від 0 до тієї точки. Для -4 ви йдете ліворуч чотири кроки, для +4 – праворуч ті ж чотири. Результат: | -4 | = 4.
Ця метафора оживає на графіку. Функція y = |x| утворює ламану з вершиною в (0,0), симетричну щодо осі Y. Ліва гілка – як дзеркальне відображення правої, ніби число “відбивається” від нуля.
Уявіть прогулянку: ви відійшли від дому 5 км на захід – відстань 5 км. Модуль перетворює напрямок на чисту величину, роблячи розрахунки універсальними.
Як обчислити модуль числа вручну: покроковий алгоритм
Обчислення модуля – справа кількох секунд, але з нюансами для складних виразів. Почніть з перевірки знаку аргументу всередині | |.
- Визначте знак числа: додатне чи нуль – копіюйте як є.
- Від’ємне – змініть знак на протилежний.
- Для виразів розкрийте умовно: знайдіть точки, де вираз =0 (критичні точки), і перевірте знаки в інтервалах.
Після списку ось таблиця з прикладами для наочності. Вона показує, як модуль поводиться з різними типами чисел.
| Число x | Знак | Модуль |x| | Пояснення |
|---|---|---|---|
| 5 | + | 5 | Додатне – без змін |
| -7.2 | – | 7.2 | -(-7.2) = 7.2 |
| 0 | 0 | 0 | Відстань до себе |
| 3/4 | + | 3/4 | Раціональне додатне |
| -√2 | – | √2 | Ірраціональне від’ємне |
Джерела даних: стандартні математичні визначення з uk.wikipedia.org. Таблиця ілюструє універсальність – від простих цілих до складних. Спробуйте самі: | -π/2 | = π/2 ≈ 1.57, бо π/2 >0.
Властивості модуля числа: правила, що спрощують життя
Модуль слухняний, як добре натренований пес: дотримується чітких правил. Перед списком ось вступ: ці властивості дозволяють маніпулювати виразами без калькулятора, економлячи час у рівняннях.
- Невід’ємність: |x| ≥ 0 для будь-якого x. Рівність – тільки при x=0.
- Модуль протилежного: |-x| = |x|. Симетрія в дії.
- Добуток: |x * y| = |x| * |y|. Знаки множаться окремо.
- Ділення: |x / y| = |x| / |y| (y ≠ 0). Аналогічно.
- Трикутна нерівність: |x + y| ≤ |x| + |y|. Коротший шлях – пряма лінія.
- Зворотна: |x + y| ≥ ||x| – |y||. Нижня межа відстані.
Ці властивості – ключ до розв’язків. Наприклад, |2 + (-3)| = | -1 | =1 ≤ |2| + | -3 | =5. Використовуйте їх для доведень і оптимізації.
Рівняння та нерівності з модулем: стратегії розв’язку
Рівняння |x – a| = b перетворюється на два: x – a = b або x – a = -b. Для x=3, |x-1|=2 дає x=3 або x=-1. Перевірте: обидва задовольняють.
Нерівності складніші: |x| < c означає -c < x < c. Для |x-2| ≤ 3 – від -1 до 5. Знайдіть критичні точки (де=0), розділіть вісь на інтервали, перевірте знак.
Ключ: модуль не може бути негативним, тож |x| = -2 – без розв’язку! Практикуйте на прикладах: розв’яжіть |2x +1| > 5 – x < -3 або x > 2.
Графік функції модуля: V-подібна краса
y = |x| – класична ламана: права гілка y=x (x≥0), ліва y=-x (x<0). Вершина в початку координат, кути 45°. Симетрія робить її парною: f(-x)=f(x).
Складніші, як y = |x^2 -1|, мають більше ламок. Графіки допомагають візуалізувати нерівності: область під кривою.
У Desmos чи GeoGebra намалюйте – побачите, як модуль “складає” графік угору.
Модуль числа в програмуванні: код, що працює миттєво
У коді модуль – must-have для відстаней, помилок чи нормалізації. Почніть з Python: вбудована функція abs(x). print(abs(-5.7)) виводить 5.7. Для комплексних – те саме.
JavaScript: Math.abs(-42) → 42. C++: std::abs з <cstdlib>. Ось приклади:
- Python: distance = abs(x2 – x1) для точок.
- JS: let mod = Math.abs(-3.14); console.log(mod); // 3.14
У геймдеві модуль векторів нормалізує напрямок. З python.org, abs() універсальна для int, float, complex.
Обчислення модуля в Excel та Google Sheets
Таблиці обожнюють модуль для фінансів чи статистики. Функція ABS(A1) поверне |значення|. =ABS(-100) =100.
Для масивів: =ABS(B1:B10). У Google Sheets те саме. Приклад: відстань між продажами – ABS(доход1 – доход2). Швидко і без помилок.
Модуль вектора та комплексного числа: розширення ідеї
Вектор у просторі – стрілка з довжиною |v| = √(x² + y² + z²). Для 2D: |(3,4)| =5, за Піфагором. Фізика: швидкість – модуль вектора швидкості.
Комплексне z = a + bi: |z| = √(a² + b²). |3 + 4i| =5. Аргумент – кут. Застосування: електротехніка, сигнали.
Застосування модуля в житті, фізиці та економіці
У повсякденні: GPS рахує |Δx| + |Δy| як манхеттенську відстань. Фізика: робота сили – модуль сили помножений на шлях. Економіка: відсоток помилки = |фактичне – планове| / планове *100%.
Програмування: нормалізація зображень, машинне навчання (L1-норма – сума модулів). Ви не повірите, але без модуля не було б точних прогнозів погоди чи маршрутів Uber.
Типові помилки при роботі з модулем
Багато хто плутає модуль з остачею від ділення – mod це інше! Друга пастка: забувають, що |x| ≥0, тож рівняння |x|= -1 без розв’язку.
- В нерівностях не ділять інтервали: для |x-1|>2 пропускають x<-1 або x>3.
- Множинні модулі: |x| + |x-2| розкривають без критичних точок (0,2).
- У коді: abs() для комплексних, але не для списків – помилка TypeError.
Перевіряйте знак аргументу перед розкриттям – це врятує 90% помилок. Практикуйте на ЗНО-прикладах, де модуль ховається в 20% задач.
Історія модуля: від латинської “міри” до сучасності
Слово “модуль” з латинської “modulus” – міра чи шаблон. Роджер Котс у 1714 ввів для комплексних, але ідея відстані – з античності. У 19 ст. стало стандартним у шкільних підручниках. В Україні – з радянських програм, де геометричний сенс пояснювали на осі.
Сьогодні модуль – у кожному смартфоні, від AI до ігор. Цікавий факт: без нього складні обчислення в квантовій механіці були б хаосом.
Експериментуйте з модулем у коді чи рівняннях – відкриєте нові горизонти. А якщо застрягли, поверніться до основ: відстань завжди позитивна.